GP2D12 Interfacing
Some time ago I bought a Sharp GP2D12 distance sensor .
There used to be a digital version of this sensor (the GP2D02, sadly discontinued) which gave the
result in digits, the analog type I got gives out a voltage. Neither of these sensors are linear, unfortunately.
So we had a look at it:

Various distances between between the sensor ( stuck to the table with play dough )
and the object ( a white cardboard box ) were taken. The voltages were measured by a digital voltmeter.
A total of 11 measurements was made.
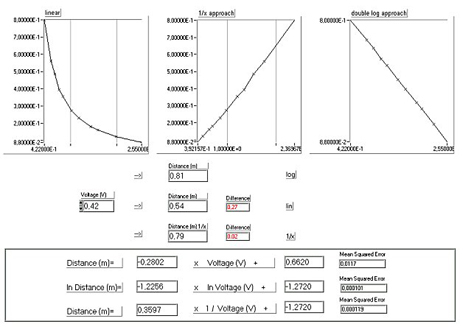
The results were plotted with a little program in Labview 5.01.
Nice graphs :) (Please click to enlarge).
When using a double logarithmic plot the result was a near perfect straight
line (3rd graphic). The equation below gives the values for the natural logarithm of distance.
The "mean squared error" is 0.0001 which is pretty good.
The only problem is that the calculation of the logarithm takes up nearly all the space of - say - an AT90S2313 ... another problem.
On Larry Barello's site
there's a far better solution to our problem:
instead of using the complicated "double log" approach Larry uses the ' 1/x ' dependancy ( 2nd graphic )
of the curve which is of course much easier to calculate. Have a look at the third equation ...
Finally a totally different approach, very feasible especially in hobby robotics:
Basically there are two informations that can be gained by a distance measurement:
- Are there any objects in the vicinity of the robot at all?
- How close are those objects exactly?
2. usually possesses no direct meaning for a robot! But should this for some reason be the case (let's say the robot does target practising) it would still be possible to do the calculations using '1 / x'. Problem solved :)